|
|
知识路径: > 计算机科学基础 > 常用数据结构 > 树 > 树和二叉树 >
|
|
考试要求:掌握
相关知识点:10个
|
|
|
|
|
|
|
|
|
.除根外的其他节点被分成n(n≥0)个不相交的集合T1,T2, …,Tn,其中每个集合本身是一棵树,树T1,T2, …,Tn称为根的子树。
|
|
|
|
这是一个递归定义,即在树的定义中又用到树的概念,它指出了树的固有特性,具有一个节点的树必然由根组成,而具有n>1个节点的树则借助于小于n个节点的树来定义。特别要注意的是递归定义中各子树T1,T2, …,Tn的相对次序是重要的,即是有序的。
|
|
|
|
|
|
|
|
|
|
.度为m的树中第i层上至多有mi-1个节点(i≥1)。
|
|
|
|
.高度为h的m叉树至多有(mh-1)/(m-1)个节点。
|
|
|
|
.具有n个节点的m叉树的最小高度为|logm(n(m-1)+1)|。
|
|
|
|
树还包含树的度、节点数及叶子节点数等。关于如何对给定的树求出满足某种条件的树的节点数和叶子节点数等问题,下面列举两个例子来加以说明。
|
|
|
|
例1:已知一棵度为m的树中有N1个度为1的节点,N2个度为2的节点,……,Nm个度为m的节点。试问该树中有多少个叶子节点?
|
|
|
解决该问题的关键是将树的节点数和树中各节点的度联系起来。若设该树中叶子节点个数为N0,则该树节点个数为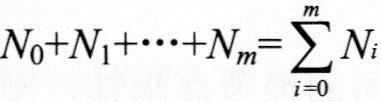 ,因该树节点个数又为 ,因该树节点个数又为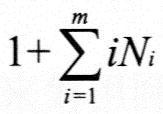 ,故 ,故
|
|
|
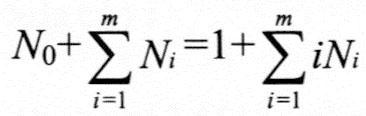 ,即 ,即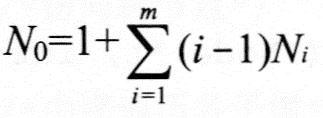
|
|
|
|
例2:已知某度为k的树中,其度为0, 1, 2, …,k-1的节点数分别为n0,n1,n2, …,nk-1,求该树的节点总数。
|
|
|
|
|
|
|
|
而树的分支数(或连线数),即n-1为:n-1=n1+2n2+(k-1)nk-1+knk,故
|
|
|
|
|